Solving the Soma cube in 3D

I bought this wooden puzzle few weeks ago from the flea market for 3 TND ($1). The build quality is quite good. It's composed of 7 different pieces that must be assembled in a 3x3x3 cube.

Solving this puzzle manually is complicated. There is no apparent solution other than brute-force. I took it to my workplace, and timed my co-workers while they reconstructed the cube. The results were irregular: fastest was 2 minutes, and slowest resolving exceeded 1 hour.

In this post, we will solve the Soma cube puzzle with PHP. According to Wikipedia, there are 240 distinct solutions (after removing all rotations and mirrors).
Here is a 3D animation on how to solve, step by step, the Soma cube in every distinct way:
If you want to know how we found those solutions, please continue reading.
First, we need to determine all the possible orientations for every piece. We will also give them labels: A, B, C, etc..
The box in red is the main box. The piece will be positioned using this box as reference.
Piece #1
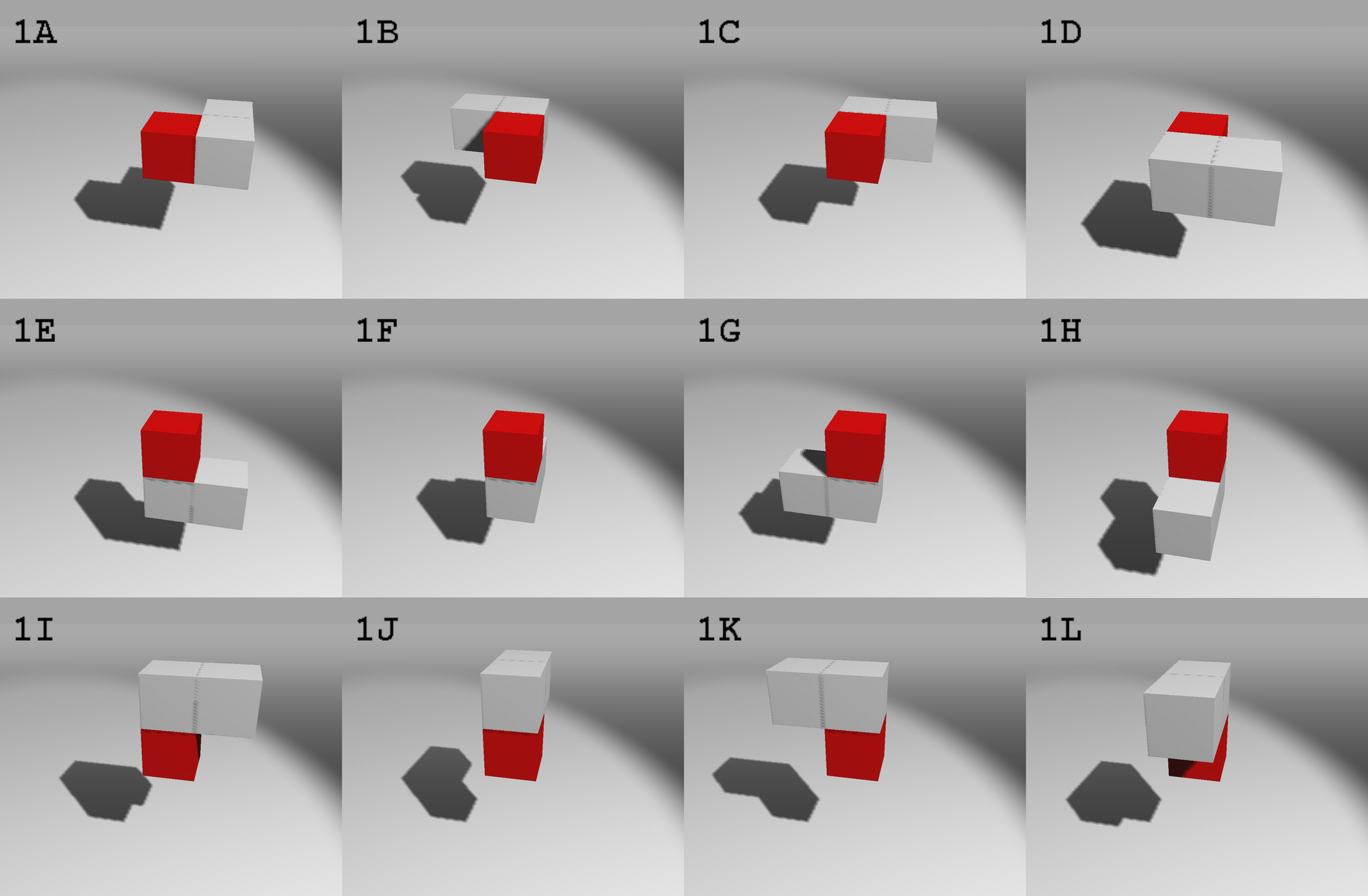
Piece #2

Piece #3
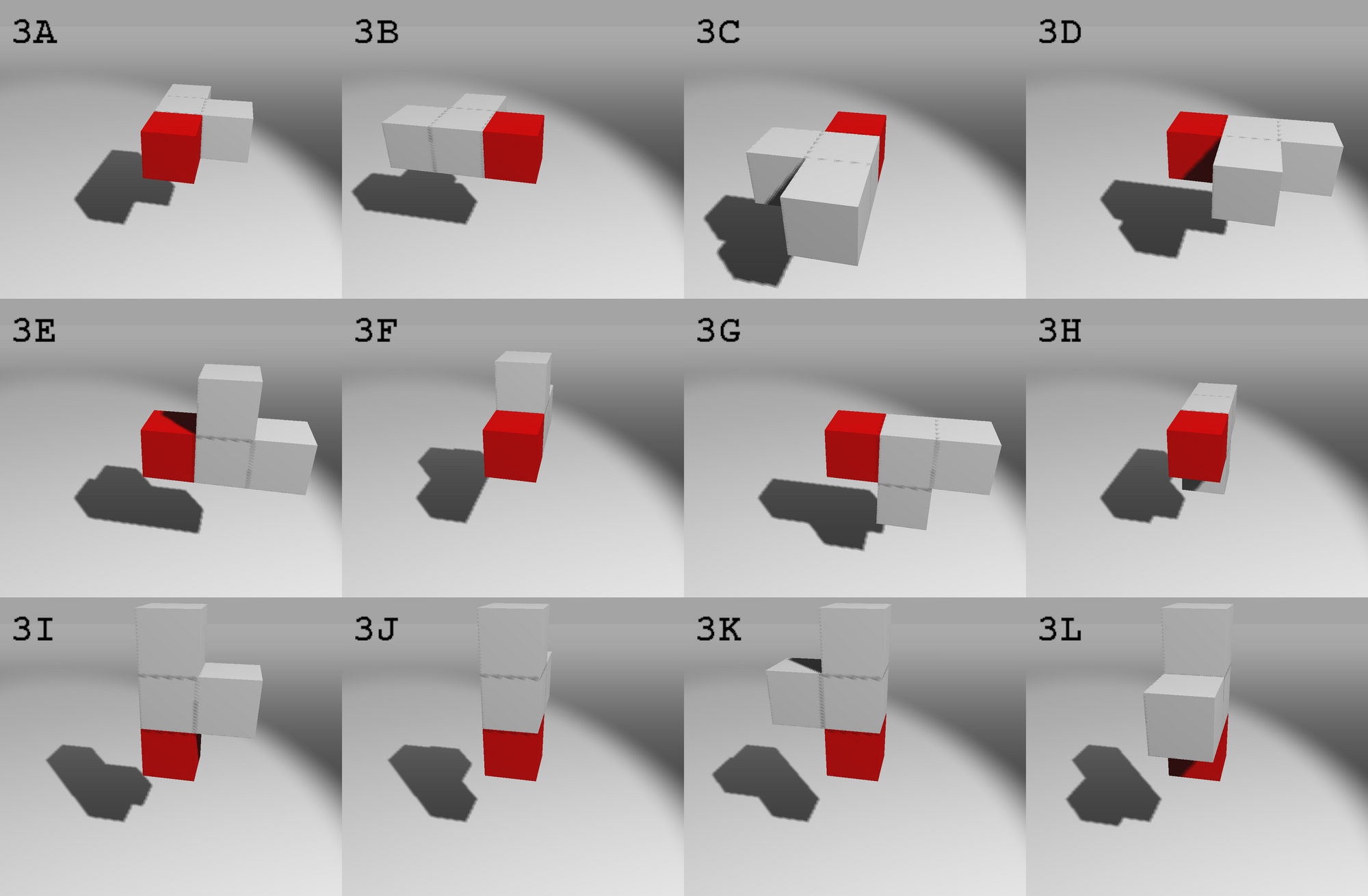
Piece #4
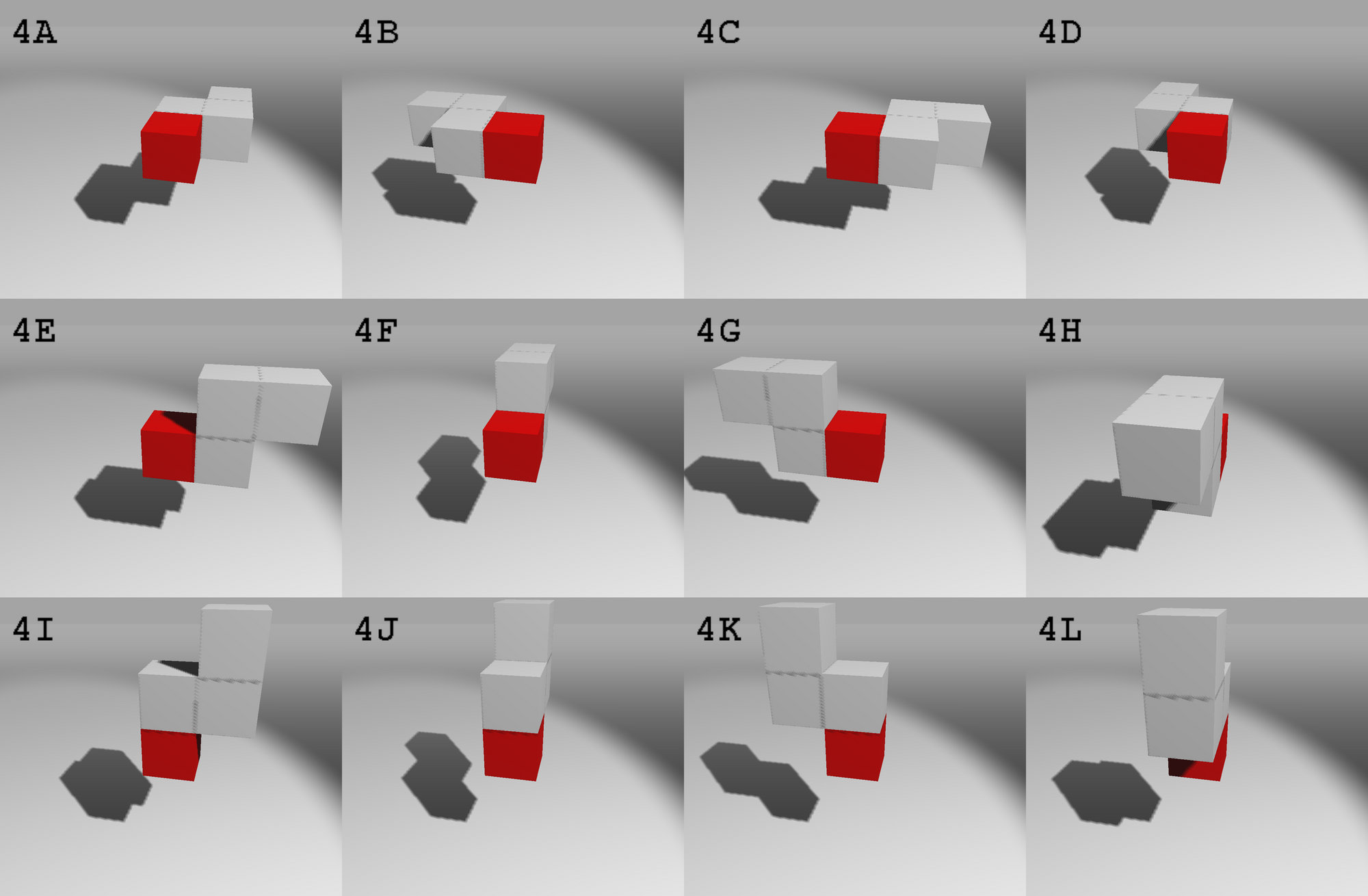
Piece #5
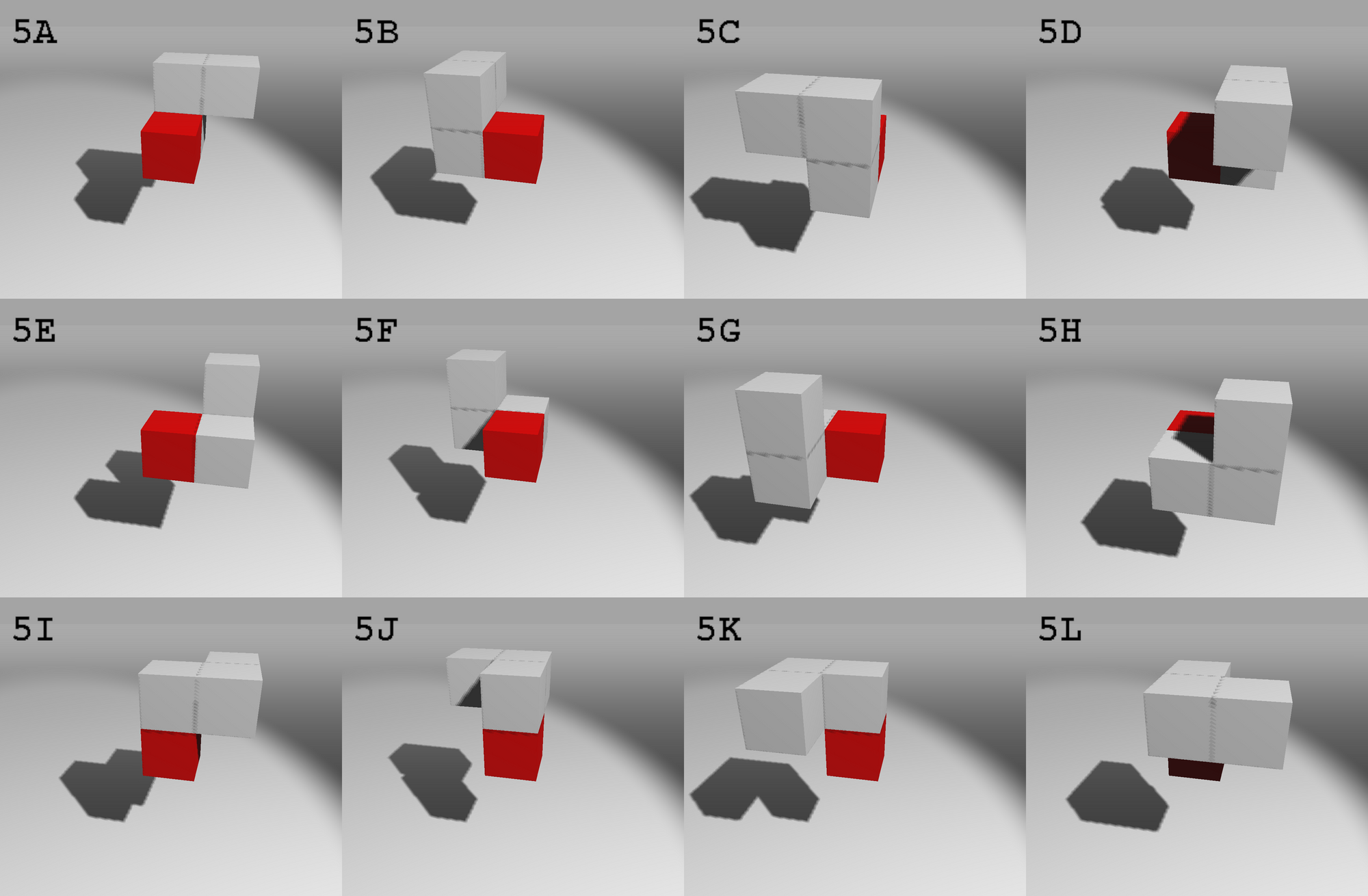
Piece #6
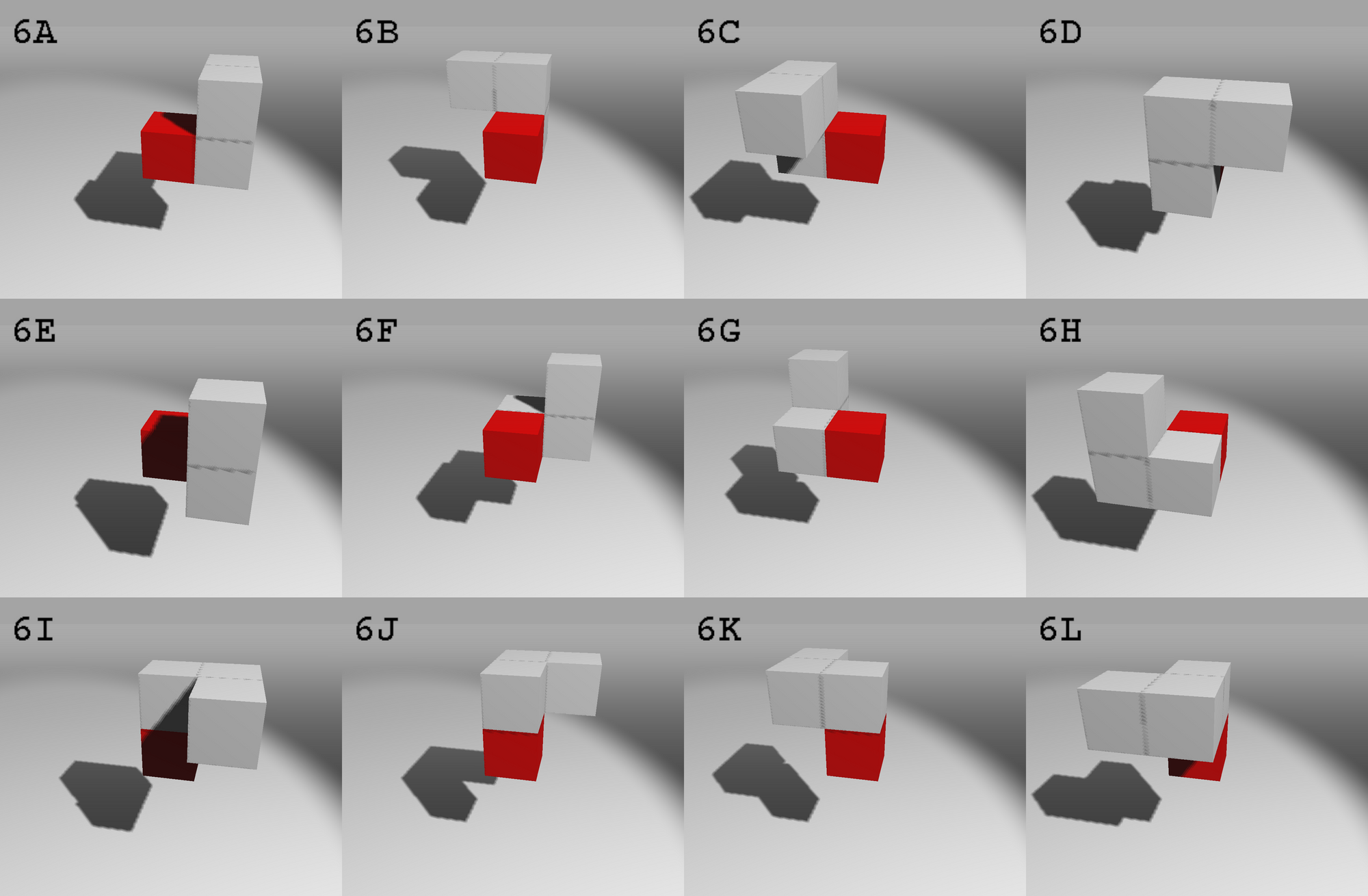
Piece #7
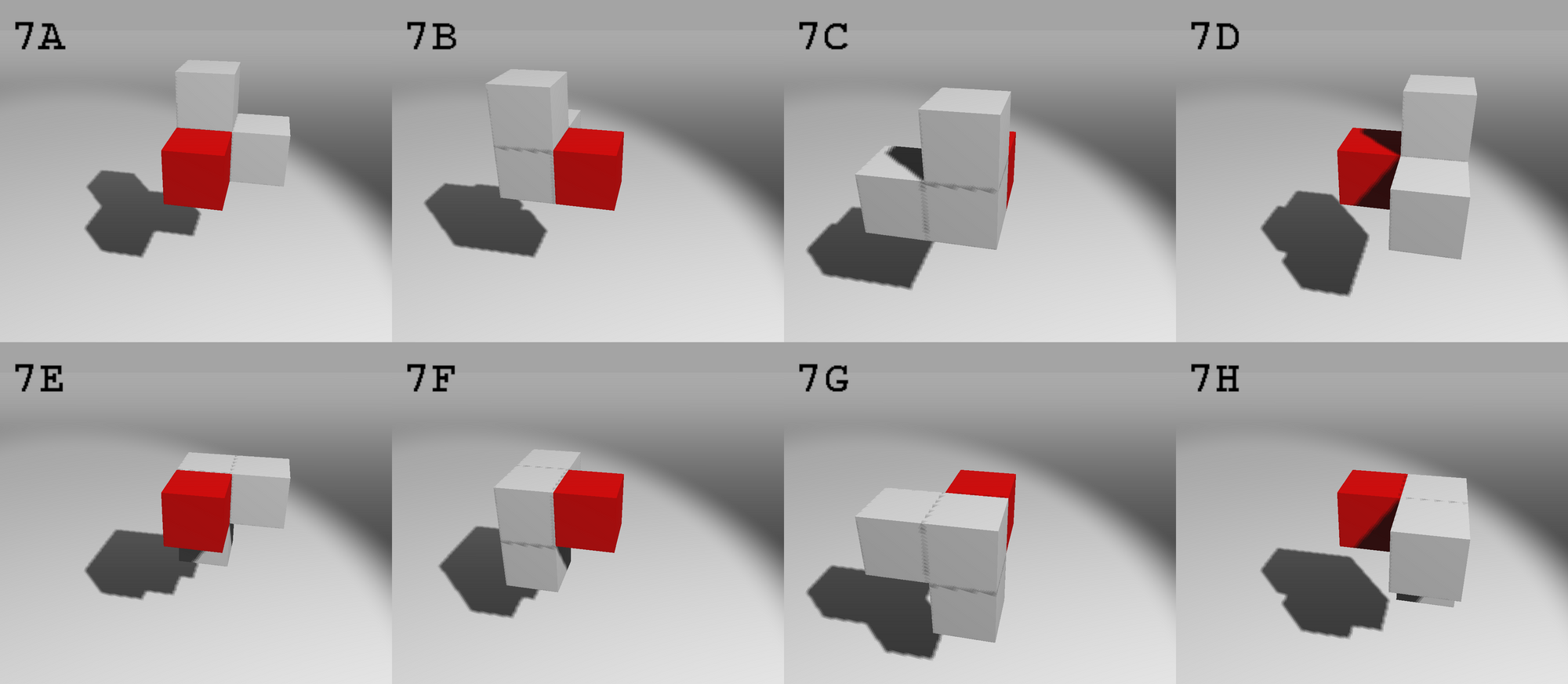
Next, we will use a backtrack algorithm to scan all the possible combinations of piece / orientation / position. A solution is detected when all of the 7 pieces are placed, with no collision, and no cube limit trespassing.
<?php
$pieces[1] = [ // half turn symmetry, half orientations (12)
// piece on horizontal plane
'A' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 1, 0] ],
'B' => [ [ 0, 0, 0], [ 0, 1, 0], [-1, 1, 0] ],
'C' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0] ],
'D' => [ [ 0, 0, 0], [ 0,-1, 0], [ 1,-1, 0] ],
// main on top
'E' => [ [ 0, 0, 0], [ 0, 0,-1], [ 1, 0,-1] ],
'F' => [ [ 0, 0, 0], [ 0, 0,-1], [ 0, 1,-1] ],
'G' => [ [ 0, 0, 0], [ 0, 0,-1], [-1, 0,-1] ],
'H' => [ [ 0, 0, 0], [ 0, 0,-1], [ 0,-1,-1] ],
// main on bottom
'I' => [ [ 0, 0, 0], [ 0, 0, 1], [ 1, 0, 1] ],
'J' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 1, 1] ],
'K' => [ [ 0, 0, 0], [ 0, 0, 1], [-1, 0, 1] ],
'L' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0,-1, 1] ],
];
$pieces[2] = [ // no symmetry, all orientations (24)
// piece on horizontal plane, inversed "L"
'A' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 1, 0], [ 1, 2, 0] ],
'B' => [ [ 0, 0, 0], [ 0, 1, 0], [-1, 1, 0], [-2, 1, 0] ],
'C' => [ [ 0, 0, 0], [-1, 0, 0], [-1,-1, 0], [-1,-2, 0] ],
'D' => [ [ 0, 0, 0], [ 0,-1, 0], [ 1,-1, 0], [ 2,-1, 0] ],
// piece on horizontal plane, correct "L"
'E' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0], [ 2, 1, 0] ],
'F' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 1, 0], [-1, 2, 0] ],
'G' => [ [ 0, 0, 0], [ 0,-1, 0], [-1,-1, 0], [-2,-1, 0] ],
'H' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1,-1, 0], [ 1,-2, 0] ],
// short leg on top
'I' => [ [ 0, 0, 0], [ 0, 0,-1], [ 1, 0,-1], [ 2, 0,-1] ],
'J' => [ [ 0, 0, 0], [ 0, 0,-1], [ 0, 1,-1], [ 0, 2,-1] ],
'K' => [ [ 0, 0, 0], [ 0, 0,-1], [-1, 0,-1], [-2, 0,-1] ],
'L' => [ [ 0, 0, 0], [ 0, 0,-1], [ 0,-1,-1], [ 0,-2,-1] ],
// short leg on bottom
'M' => [ [ 0, 0, 0], [ 0, 0, 1], [ 1, 0, 1], [ 2, 0, 1] ],
'N' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 1, 1], [ 0, 2, 1] ],
'O' => [ [ 0, 0, 0], [ 0, 0, 1], [-1, 0, 1], [-2, 0, 1] ],
'P' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0,-1, 1], [ 0,-2, 1] ],
// long leg on top
'Q' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 0, 1], [ 1, 0, 2] ],
'R' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 1, 1], [ 0, 1, 2] ],
'S' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 0, 1], [-1, 0, 2] ],
'T' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-1, 1], [ 0,-1, 2] ],
// long leg on bottom
'U' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 0,-1], [ 1, 0,-2] ],
'V' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 1,-1], [ 0, 1,-2] ],
'W' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 0,-1], [-1, 0,-2] ],
'X' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-1,-1], [ 0,-1,-2] ],
];
$pieces[3] = [ // half turn symmetry, half orientations (12)
// piece on horizontal plane, "T"
'A' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 2, 0], [ 1, 1, 0] ],
'B' => [ [ 0, 0, 0], [-1, 0, 0], [-2, 0, 0], [-1, 1, 0] ],
'C' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-2, 0], [-1,-1, 0] ],
'D' => [ [ 0, 0, 0], [ 1, 0, 0], [ 2, 0, 0], [ 1,-1, 0] ],
// "T" leg on top
'E' => [ [ 0, 0, 0], [ 1, 0, 0], [ 2, 0, 0], [ 1, 0, 1] ],
'F' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 2, 0], [ 0, 1, 1] ],
// "T" leg on bottom
'G' => [ [ 0, 0, 0], [ 1, 0, 0], [ 2, 0, 0], [ 1, 0,-1] ],
'H' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 2, 0], [ 0, 1,-1] ],
// "T" leg horizontal (4 directions)
'I' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 0, 2], [ 1, 0, 1] ],
'J' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 0, 2], [ 0, 1, 1] ],
'K' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 0, 2], [-1, 0, 1] ],
'L' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 0, 2], [ 0,-1, 1] ],
];
$pieces[4] = [ // half turn symmetry, half orientations (12)
// piece on horizontal plane
'A' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0], [ 1, 2, 0] ],
'B' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 1, 0], [-2, 1, 0] ],
// piece on horizontal plane (flipped)
'C' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 1, 0], [ 2, 1, 0] ],
'D' => [ [ 0, 0, 0], [ 0, 1, 0], [-1, 1, 0], [-1, 2, 0] ],
// piece standing on 2 boxes
'E' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 0, 1], [ 2, 0, 1] ],
'F' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 1, 1], [ 0, 2, 1] ],
'G' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 0, 1], [-2, 0, 1] ],
'H' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-1, 1], [ 0,-2, 1] ],
// piece standing on 1 box
'I' => [ [ 0, 0, 0], [ 0, 0, 1], [ 1, 0, 1], [ 1, 0, 2] ],
'J' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 1, 1], [ 0, 1, 2] ],
'K' => [ [ 0, 0, 0], [ 0, 0, 1], [-1, 0, 1], [-1, 0, 2] ],
'L' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0,-1, 1], [ 0,-1, 2] ],
];
$pieces[5] = [ // half turn symmetry, half orientations (12)
// piece standing on 2 boxes
'A' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 1, 1], [ 1, 1, 1] ],
'B' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 0, 1], [-1, 1, 1] ],
'C' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-1, 1], [-1,-1, 1] ],
'D' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 0, 1], [ 1,-1, 1] ],
// piece standing on 3 boxes
'E' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 1, 0], [ 1, 1, 1] ],
'F' => [ [ 0, 0, 0], [ 0, 1, 0], [-1, 1, 0], [-1, 1, 1] ],
'G' => [ [ 0, 0, 0], [-1, 0, 0], [-1,-1, 0], [-1,-1, 1] ],
'H' => [ [ 0, 0, 0], [ 0,-1, 0], [ 1,-1, 0], [ 1,-1, 1] ],
// piece standing on 1 box
'I' => [ [ 0, 0, 0], [ 0, 0, 1], [ 1, 0, 1], [ 1, 1, 1] ],
'J' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 1, 1], [-1, 1, 1] ],
'K' => [ [ 0, 0, 0], [ 0, 0, 1], [-1, 0, 1], [-1,-1, 1] ],
'L' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0,-1, 1], [ 1,-1, 1] ],
];
$pieces[6] = [ // half turn symmetry, half orientations (12)
// piece standing on 2 boxes
'A' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1, 0, 1], [ 1, 1, 1] ],
'B' => [ [ 0, 0, 0], [ 0, 1, 0], [ 0, 1, 1], [-1, 1, 1] ],
'C' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 0, 1], [-1,-1, 1] ],
'D' => [ [ 0, 0, 0], [ 0,-1, 0], [ 0,-1, 1], [ 1,-1, 1] ],
// piece standing on 3 boxes
'E' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1,-1, 0], [ 1,-1, 1] ],
'F' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0], [ 1, 1, 1] ],
'G' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 1, 0], [-1, 1, 1] ],
'H' => [ [ 0, 0, 0], [ 0,-1, 0], [-1,-1, 0], [-1,-1, 1] ],
// piece standing on 1 box
'I' => [ [ 0, 0, 0], [ 0, 0, 1], [ 1, 0, 1], [ 1,-1, 1] ],
'J' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0, 1, 1], [ 1, 1, 1] ],
'K' => [ [ 0, 0, 0], [ 0, 0, 1], [-1, 0, 1], [-1, 1, 1] ],
'L' => [ [ 0, 0, 0], [ 0, 0, 1], [ 0,-1, 1], [-1,-1, 1] ],
];
$pieces[7] = [ // 1/3 turn symmetry, 1/3 orientations (8)
// piece standing on 3 boxes
'A' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0], [ 0, 1, 1] ],
'B' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 1, 0], [-1, 0, 1] ],
'C' => [ [ 0, 0, 0], [ 0,-1, 0], [-1,-1, 0], [ 0,-1, 1] ],
'D' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1,-1, 0], [ 1, 0, 1] ],
// piece standing on 1 box
'E' => [ [ 0, 0, 0], [ 0, 1, 0], [ 1, 1, 0], [ 0, 1,-1] ],
'F' => [ [ 0, 0, 0], [-1, 0, 0], [-1, 1, 0], [-1, 0,-1] ],
'G' => [ [ 0, 0, 0], [ 0,-1, 0], [-1,-1, 0], [ 0,-1,-1] ],
'H' => [ [ 0, 0, 0], [ 1, 0, 0], [ 1,-1, 0], [ 1, 0,-1] ],
];
$grid = initializeGrid();
$solutions = [];
$moves = [];
// start the backtrack
placePiece($grid, $pieces, $moves, $solutions);
// save the solutions in a file
file_put_contents("solutions.txt", serialize($solutions));
exit();
/////////////////////////////
// FUNCTIONS
/////////////////////////////
function initializeGrid() {
$grid = [];
for ($i = 0; $i < 3 ; $i++) {
for ($j = 0; $j < 3 ; $j++) {
for ($k = 0; $k < 3 ; $k++) {
$grid[$i][$j][$k] = null;
}
}
}
return $grid;
}
function placePiece($grid, $remainingPieces, $moves, &$solutions) {
reset($remainingPieces);
$pieceNumber = key($remainingPieces);
$piece = current($remainingPieces);
unset($remainingPieces[$pieceNumber]);
foreach ($piece as $orientationLabel => $boxes) {
for ($i = 0; $i < 3 ; $i++) {
for ($j = 0; $j < 3 ; $j++) {
for ($k = 0; $k < 3 ; $k++) {
$tempBoxes = [];
foreach ($boxes as $box) {
$tempBox = [];
$tempBox[0] = $box[0] + $i;
$tempBox[1] = $box[1] + $j;
$tempBox[2] = $box[2] + $k;
$tempBoxes[] = $tempBox;
}
// check current gird integrity
foreach ($tempBoxes as $tempBox) {
if (!checkGridLimit($tempBox)) {
// the piece is trespassing the 3x3x3 cube limits
continue 2;
}
if (!checkCollision($grid, $tempBox)) {
// the is a collision between 2 pieces
continue 2;
}
}
// update grid
$tempGrid = updateGrid($grid, $tempBoxes, $pieceNumber);
$move = [
'piece' => $pieceNumber,
'orientation' => $orientationLabel,
'boxes' => $tempBoxes,
'x' => $i,
'y' => $j,
'z' => $k,
];
$currentMoves = $moves;
$currentMoves[] = $move;
// next step
if (empty($remainingPieces)) {
$sortedMoves = sortAllMoves($tempGrid, $currentMoves);
$movesString = "";
foreach ($sortedMoves as $move) {
$movesString .= $move['piece'] . $move['orientation'].":(".$move['x'].",".$move['y'].",".$move['z'].") ";
}
$solution = [];
$solution['moves'] = $movesString;
$solution['grid'] = $tempGrid;
$solutions[] = $solution;
print("Solution : $movesString\n");
} else {
placePiece($tempGrid, $remainingPieces, $currentMoves, $solutions);
}
}
}
}
}
}
function checkGridLimit($box) {
// check x
if (($box[0] < 0) or ($box[0] > 2)) {
return false;
}
// check y
if (($box[1] < 0) or ($box[1] > 2)) {
return false;
}
// check z
if (($box[2] < 0) or ($box[2] > 2)) {
return false;
}
return true;
}
function checkCollision($grid, $box) {
$x = $box[0];
$y = $box[1];
$z = $box[2];
return is_null($grid[$x][$y][$z]);
}
function updateGrid($grid, $boxes, $pieceNumber) {
// place piece number in each box
foreach ($boxes as $box) {
$x = $box[0];
$y = $box[1];
$z = $box[2];
$grid[$x][$y][$z] = $pieceNumber;
}
return $grid;
}
// sort the moves so that the pieces could be placed vertically
function sortAllMoves($grid, $moves) {
$dependencies = [];
for ($i = 1; $i <= 7; $i++) {
$dependencies[$i] = [];
}
for ($x = 0; $x < 3 ; $x++) {
for ($y = 0; $y < 3 ; $y++) {
for ($z = 1; $z < 3 ; $z++) {
$pieceTop = $grid[$x][$y][$z];
$pieceBottom = $grid[$x][$y][$z-1];
if ($pieceTop != $pieceBottom and !in_array($pieceBottom, $dependencies[$pieceTop])) {
$dependencies[$pieceTop][] = $pieceBottom;
}
}
}
}
$sortedPieces = [];
while (count($sortedPieces) < 7) {
for ($piece = 1; $piece <= 7; $piece++) {
if (!in_array($piece, $sortedPieces)) {
foreach ($dependencies[$piece] as $dependentPiece) {
// checking if there is a dependent piece not yet placed
if (!in_array($dependentPiece, $sortedPieces)) {
continue 2;
}
}
$sortedPieces[] = $piece;
}
}
}
$sortedMoves = [];
foreach ($sortedPieces as $piece) {
$sortedMoves[] = $moves[$piece - 1];
}
return $sortedMoves;
}
After the script finishes executing, we get 11520 solutions. This number must be reduced to 240. We need to remove all rotations and mirrors. For each distinct solution, there are 24 rotation. Also, each solution has a mirror (240 x 24 x 2 = 11520).
Please notice that when mirroring, all the pieces could be mirror of themselves, except the #5 and the #6. Those 2 pieces must exchange position to make the mirror possible.

Removing the rotations and the mirrors simultaneously did not work. So, we regrouped all of the rotations in clusters. In total, we got 480 clusters. Each cluster is composed of 24 rotation of the same solution. After that, we remove the mirror clusters. And finally, we keep the first solution of each cluster.
<?php
// loading the 11520 solutions from the file
if (!file_exists("solutions.txt")) {
die("Error: solutions file is missing.\n");
}
$solutions = unserialize(file_get_contents("solutions.txt"));
$rotationClusters = [];
while (!empty($solutions)) {
$solution = array_shift($solutions);
$cluster = getRotationCluster($solutions, $solution);
print("Cluster Size : " . count($cluster)."\n");
$rotationClusters[] = $cluster;
}
print("Total Number of clusters : " . count($rotationClusters)."\n\n");
sleep(1);
print("Removing mirrored clusters\n");
$distinctClusters = [];
while (!empty($rotationClusters)) {
$cluster = array_shift($rotationClusters);
$distinctClusters[] = $cluster;
removeMirrorCluster($rotationClusters, $cluster);
}
print("Distinct clusters : " . count($distinctClusters)."\n\n");
// display a solution from every cluster
foreach ($distinctClusters as $cluster) {
print($cluster[0]['moves']."\n");
}
exit();
///////////////////////////
// FUNCTIONS
///////////////////////////
// return an array of all the different rotations of a solution
function getRotationCluster(&$solutions, $chosenSolution) {
$cluster = [$chosenSolution];
foreach ($solutions as $key => $solution) {
if (rotationGrid($solution['grid'], $chosenSolution['grid'])) {
unset($solutions[$key]);
$cluster[] = $solution;
}
}
return $cluster;
}
// for each cluster, find the mirror cluster and remove it
function removeMirrorCluster(&$clusters, $chosenCluster) {
$chosenSolution = array_shift($chosenCluster);
foreach ($clusters as $key => $cluster) {
foreach ($cluster as $solution) {
if (mirrorGrid($solution['grid'], $chosenSolution['grid'])) {
unset($clusters[$key]);
print("mirror found\n");
return;
}
}
}
print("mirror not found\n");
displayGrid($chosenSolution['grid']);
print($chosenSolution['moves']);
exit();
}
function mirrorGrid($grid1, $grid2) {
for ($i = 0; $i < 3; $i++) {
for ($j = 0; $j < 3; $j++) {
for ($k = 0; $k < 3; $k++) {
switch ($grid1[$i][$j][$k]) {
// if piece #5 or #6, check if the mirror has the alternate piece
case 5:
if ($grid2[$i][$j][2 - $k] != 6) {
return false;
}
break;
case 6:
if ($grid2[$i][$j][2 - $k] != 5) {
return false;
}
break;
default:
if ($grid2[$i][$j][2 - $k] != $grid1[$i][$j][$k]) {
return false;
}
break;
}
}
}
}
return true;
}
function rotationGrid($grid1, $grid2) {
// 24 possible rotations
for ($rotation = 0; $rotation < 24; $rotation++) {
for ($i = 0; $i < 3; $i++) {
for ($j = 0; $j < 3; $j++) {
for ($k = 0; $k < 3; $k++) {
switch ($rotation) {
case 0:
if ($grid1[$i][$j][$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 1:
if ($grid1[2-$k][$j][$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 2:
if ($grid1[2-$i][$j][2-$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 3:
if ($grid1[$k][$j][2-$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 4:
if ($grid1[$j][2-$i][$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 5:
if ($grid1[$j][$k][$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 6:
if ($grid1[$j][$i][2-$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 7:
if ($grid1[$j][2-$k][2-$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 8:
if ($grid1[2-$j][$i][$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 9:
if ($grid1[2-$j][2-$k][$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 10:
if ($grid1[2-$j][2-$i][2-$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 11:
if ($grid1[2-$j][$k][2-$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 12:
if ($grid1[$i][$k][2-$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 13:
if ($grid1[2-$k][$i][2-$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 14:
if ($grid1[2-$i][2-$k][2-$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 15:
if ($grid1[$k][2-$i][2-$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 16:
if ($grid1[$i][2-$j][2-$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 17:
if ($grid1[2-$k][2-$j][2-$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 18:
if ($grid1[2-$i][2-$j][$k] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 19:
if ($grid1[$k][2-$j][$i] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 20:
if ($grid1[$i][2-$k][$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 21:
if ($grid1[2-$k][2-$i][$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 22:
if ($grid1[2-$i][$k][$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
case 23:
if ($grid1[$k][$i][$j] != $grid2[$i][$j][$k]) {
continue 5;
}
break;
default:
die("not supposed to happen\n");
break;
}
}
}
}
return true;
}
return false;
}
Down here, the 240 distinct solutions. Each piece should be positioned by placing its main box in the indicated position (x,y,z).
1A:(0,0,0) 6K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5A:(0,1,0) 4F:(0,0,1) 2A:(0,0,2)
1A:(0,0,0) 3K:(2,0,0) 7D:(1,2,0) 5A:(0,1,0) 6A:(1,1,1) 4F:(0,0,1) 2A:(0,0,2)
1A:(0,0,0) 3E:(0,2,0) 4L:(0,1,0) 5C:(2,1,0) 6H:(2,2,1) 7E:(0,1,2) 2A:(1,0,2)
1A:(0,0,0) 2B:(2,1,0) 5J:(2,0,0) 6J:(0,1,0) 7H:(1,2,2) 4E:(0,0,1) 3A:(0,0,2)
1A:(0,0,0) 2B:(2,1,0) 4J:(2,0,0) 5L:(0,1,0) 6F:(1,1,1) 7E:(0,1,2) 3B:(2,0,2)
1A:(0,0,0) 2B:(2,1,0) 4J:(0,1,0) 5F:(2,1,1) 6K:(2,0,0) 7F:(1,0,2) 3C:(2,2,2)
1A:(0,0,0) 2B:(2,1,0) 4J:(2,0,0) 7E:(0,0,1) 3G:(0,0,2) 6C:(1,2,1) 5K:(2,2,1)
1A:(0,0,0) 2B:(2,1,0) 3J:(2,0,0) 5L:(0,1,0) 6F:(1,1,1) 7E:(0,1,2) 4C:(0,0,2)
1A:(0,0,0) 2B:(2,1,0) 3K:(2,0,0) 5E:(1,1,1) 6J:(0,1,0) 7F:(1,0,2) 4B:(2,1,2)
1A:(0,0,0) 2B:(2,1,0) 3K:(2,0,0) 4L:(0,1,0) 6C:(2,1,1) 5D:(1,2,1) 7E:(0,1,2)
1A:(0,0,0) 2B:(2,1,0) 3K:(2,0,0) 4L:(0,1,0) 6F:(1,1,1) 7E:(0,1,2) 5K:(2,1,1)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 7F:(1,1,1) 2B:(2,1,2) 5B:(1,0,1) 6K:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 4C:(0,1,1) 5B:(1,0,1) 6K:(2,0,1) 2B:(2,1,2)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 7F:(1,1,1) 2B:(2,1,2) 5B:(1,0,1) 6K:(2,0,1)
1A:(0,0,0) 4L:(0,1,0) 7D:(1,2,0) 3J:(2,0,0) 6I:(0,2,0) 2B:(2,1,2) 5J:(1,0,1)
1A:(0,0,0) 3K:(2,0,0) 7D:(1,2,0) 5A:(0,1,0) 6D:(0,1,1) 4G:(2,1,1) 2B:(2,1,2)
1A:(0,0,0) 4K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5A:(0,1,0) 6F:(0,0,1) 2C:(1,2,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 3J:(2,0,0) 6I:(0,2,0) 2C:(1,2,2) 4A:(1,0,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 4J:(2,0,0) 6I:(0,2,0) 2D:(0,1,2) 3D:(0,2,2)
1A:(0,0,0) 5C:(2,1,0) 7A:(0,1,0) 4L:(2,2,0) 6F:(0,0,1) 2D:(0,1,2) 3G:(0,2,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 3I:(0,2,0) 4J:(2,0,0) 6J:(1,1,1) 2D:(0,1,2)
1A:(0,0,0) 2E:(0,1,0) 4F:(2,0,0) 5G:(1,2,1) 6H:(1,1,1) 7G:(2,1,2) 3D:(0,2,2)
1A:(0,0,0) 2E:(0,1,0) 4F:(2,0,0) 5H:(0,2,1) 6A:(1,0,1) 7F:(1,0,2) 3G:(0,2,2)
1A:(0,0,0) 2E:(0,1,0) 4F:(2,0,0) 6A:(1,0,1) 7B:(1,1,1) 3G:(0,2,2) 5I:(0,0,1)
1A:(0,0,0) 2E:(0,1,0) 4C:(0,1,1) 5C:(2,1,0) 6I:(0,2,1) 7F:(1,0,2) 3H:(2,0,2)
1A:(0,0,0) 2E:(0,1,0) 3K:(2,0,0) 4J:(2,1,0) 6D:(1,2,1) 5A:(0,1,1) 7F:(1,0,2)
1A:(0,0,0) 2E:(0,1,0) 3K:(2,0,0) 4J:(2,1,0) 6G:(1,1,1) 7F:(1,0,2) 5L:(1,2,1)
1A:(0,0,0) 2E:(0,1,0) 3K:(2,0,0) 4K:(2,1,0) 5D:(1,2,1) 6D:(0,1,1) 7E:(0,1,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 4J:(2,0,0) 6I:(0,2,0) 2E:(0,1,2) 3B:(2,0,2)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 6A:(1,0,1) 7F:(1,1,1) 2E:(0,1,2) 5I:(0,0,1)
1A:(0,0,0) 3F:(2,0,0) 6A:(1,0,1) 7A:(0,1,0) 4C:(0,1,1) 5I:(0,0,1) 2E:(0,1,2)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 6A:(1,0,1) 7F:(1,1,1) 2E:(0,1,2) 5I:(0,0,1)
1A:(0,0,0) 7D:(1,2,0) 4J:(2,0,0) 5A:(0,1,0) 6F:(0,0,1) 2E:(0,1,2) 3G:(0,0,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 3J:(2,0,0) 6I:(0,2,0) 2E:(0,1,2) 4C:(0,0,2)
1A:(0,0,0) 3K:(2,0,0) 4L:(0,1,0) 7D:(1,2,0) 6I:(0,2,0) 2E:(0,1,2) 5K:(2,1,1)
1A:(0,0,0) 3F:(2,0,0) 6A:(1,0,1) 7A:(0,1,0) 4A:(0,0,1) 5K:(2,2,1) 2F:(1,0,2)
1A:(0,0,0) 3F:(2,0,0) 4H:(0,2,0) 6A:(1,0,1) 7H:(0,2,1) 2F:(1,0,2) 5K:(2,2,1)
1A:(0,0,0) 4H:(0,2,0) 6K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5D:(0,2,1) 2F:(1,0,2)
1A:(0,0,0) 5C:(2,1,0) 7A:(0,1,0) 4K:(2,2,0) 6F:(0,0,1) 2F:(1,0,2) 3H:(2,0,2)
1A:(0,0,0) 3K:(2,0,0) 4H:(0,2,0) 7D:(1,2,0) 6A:(1,1,1) 5D:(0,2,1) 2F:(1,0,2)
1A:(0,0,0) 3K:(2,0,0) 4H:(0,2,0) 7D:(1,2,0) 6E:(0,2,1) 2F:(1,0,2) 5J:(2,1,1)
1A:(0,0,0) 3F:(2,0,0) 5H:(1,1,1) 7A:(0,1,0) 4G:(2,2,1) 6D:(0,1,1) 2G:(2,2,2)
1A:(0,0,0) 3K:(2,0,0) 5C:(2,2,0) 7A:(0,1,0) 4G:(2,2,1) 6D:(0,1,1) 2G:(2,2,2)
1A:(0,0,0) 2H:(1,2,0) 4H:(0,2,0) 5E:(1,0,1) 6F:(1,1,1) 7E:(0,1,2) 3B:(2,0,2)
1A:(0,0,0) 2H:(1,2,0) 4H:(0,2,0) 5F:(2,0,1) 6C:(1,2,1) 7H:(1,2,2) 3G:(0,0,2)
1A:(0,0,0) 2H:(1,2,0) 4H:(0,2,0) 6C:(1,2,1) 7D:(1,1,1) 3G:(0,0,2) 5K:(2,2,1)
1A:(0,0,0) 2H:(1,2,0) 4C:(0,0,1) 5A:(0,1,0) 6K:(2,0,1) 7H:(1,2,2) 3H:(0,0,2)
1A:(0,0,0) 2H:(1,2,0) 3I:(0,2,0) 4I:(0,1,0) 5B:(1,0,1) 6B:(2,1,1) 7G:(2,1,2)
1A:(0,0,0) 2H:(1,2,0) 3I:(0,2,0) 4L:(0,1,0) 6B:(1,0,1) 5C:(2,1,1) 7H:(1,2,2)
1A:(0,0,0) 2H:(1,2,0) 3I:(0,2,0) 4L:(0,1,0) 6E:(1,1,1) 7H:(1,2,2) 5J:(1,0,1)
1A:(0,0,0) 3E:(0,2,0) 4J:(0,1,0) 5C:(2,1,0) 6H:(2,2,1) 7F:(1,0,2) 2H:(1,2,2)
1A:(0,0,0) 2I:(0,2,1) 4F:(2,0,0) 5I:(0,1,0) 6A:(1,0,1) 7F:(1,0,2) 3D:(0,2,2)
1A:(0,0,0) 2I:(0,2,1) 4F:(2,0,0) 6I:(0,1,0) 7F:(1,0,2) 3G:(0,2,2) 5J:(2,0,1)
1A:(0,0,0) 2I:(0,2,1) 4F:(2,0,0) 7E:(0,0,1) 3G:(0,2,2) 5J:(2,0,1) 6K:(1,0,1)
1A:(0,0,0) 3F:(2,0,0) 5G:(1,2,0) 6H:(1,1,1) 7G:(2,1,2) 2I:(0,2,2) 4C:(0,1,2)
1A:(0,0,0) 3F:(2,0,0) 5H:(1,1,1) 6F:(0,1,0) 7H:(1,2,2) 2J:(0,0,2) 4D:(1,0,2)
1A:(0,0,0) 3K:(2,0,0) 5C:(2,2,0) 6F:(0,1,0) 7H:(1,2,2) 2J:(0,0,2) 4D:(1,0,2)
1A:(0,0,0) 2J:(2,0,1) 7A:(0,1,0) 4A:(0,0,1) 6B:(2,1,1) 3A:(0,0,2) 5I:(1,0,1)
1A:(0,0,0) 2J:(2,0,1) 4H:(0,2,0) 7H:(0,2,1) 3A:(0,0,2) 6B:(2,1,1) 5I:(1,0,1)
1A:(0,0,0) 2J:(2,0,1) 4C:(0,0,1) 7A:(0,1,0) 3B:(2,0,2) 5D:(1,2,1) 6J:(0,1,1)
1A:(0,0,0) 2J:(2,0,1) 4C:(0,0,1) 5G:(1,2,0) 6C:(1,2,1) 7H:(1,2,2) 3B:(2,0,2)
1A:(0,0,0) 2J:(2,0,1) 4E:(0,2,0) 5L:(0,1,0) 6A:(1,1,1) 7E:(0,1,2) 3B:(2,0,2)
1A:(0,0,0) 2J:(2,0,1) 4A:(1,0,1) 6F:(0,1,0) 3C:(2,2,2) 5A:(0,1,1) 7F:(1,0,2)
1A:(0,0,0) 2J:(2,0,1) 4A:(1,0,1) 7A:(0,1,0) 3C:(2,2,2) 6D:(0,1,1) 5K:(1,2,1)
1A:(0,0,0) 2J:(2,0,1) 4H:(0,2,0) 5C:(1,1,1) 6I:(1,2,0) 7E:(0,1,2) 3C:(2,2,2)
1A:(0,0,0) 2J:(2,0,1) 7A:(0,1,0) 4C:(0,1,1) 5B:(1,0,1) 6L:(2,1,1) 3D:(0,2,2)
1A:(0,0,0) 2J:(2,0,1) 4E:(0,2,0) 7F:(1,1,1) 3D:(0,2,2) 5B:(1,0,1) 6L:(2,1,1)
1A:(0,0,0) 2J:(2,0,1) 7A:(0,1,0) 4G:(2,2,1) 6A:(1,1,1) 5A:(0,0,1) 3G:(0,0,2)
1A:(0,0,0) 2J:(2,0,1) 4H:(0,2,0) 6I:(1,2,0) 7E:(0,1,2) 3G:(0,0,2) 5I:(1,1,1)
1A:(0,0,0) 2J:(2,0,1) 4H:(0,2,0) 5L:(1,2,0) 6L:(2,2,1) 7E:(0,1,2) 3G:(0,0,2)
1A:(0,0,0) 2J:(2,0,1) 4E:(0,0,1) 7A:(0,1,0) 6C:(1,1,1) 5C:(2,2,1) 3G:(0,2,2)
1A:(0,0,0) 2J:(2,0,1) 4H:(2,2,1) 7A:(0,1,0) 5A:(1,1,1) 6A:(0,0,1) 3H:(0,0,2)
1A:(0,0,0) 2J:(2,0,1) 4E:(0,2,0) 6I:(0,1,0) 7E:(0,1,2) 3H:(2,0,2) 5I:(0,0,1)
1A:(0,0,0) 2J:(2,0,1) 4E:(0,2,0) 5L:(0,1,0) 6L:(1,1,1) 7E:(0,1,2) 3H:(2,0,2)
1A:(0,0,0) 2J:(2,0,1) 7A:(0,1,0) 4F:(0,0,1) 5C:(1,1,1) 6C:(2,2,1) 3H:(2,0,2)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 2K:(2,0,2) 5L:(0,1,1) 6F:(1,1,1) 4B:(2,1,2)
1A:(0,0,0) 3F:(2,0,0) 5G:(1,2,0) 6F:(1,1,1) 7E:(0,1,2) 2K:(2,0,2) 4C:(0,0,2)
1A:(0,0,0) 6B:(2,0,0) 7A:(0,1,0) 2K:(2,0,2) 3K:(2,2,0) 4B:(2,1,2) 5L:(0,1,1)
1A:(0,0,0) 5G:(1,2,0) 6B:(2,0,0) 2K:(2,0,2) 3K:(2,2,0) 4C:(0,0,2) 7E:(0,1,2)
1A:(0,0,0) 2K:(2,2,1) 4E:(0,2,1) 5C:(2,1,0) 6L:(2,1,1) 7E:(0,0,1) 3A:(0,0,2)
1A:(0,0,0) 2K:(2,2,1) 4E:(0,2,1) 5L:(0,1,0) 6B:(2,0,0) 7G:(2,1,2) 3A:(0,0,2)
1A:(0,0,0) 2K:(2,2,1) 4J:(0,1,0) 5C:(2,1,0) 6G:(2,1,1) 7F:(1,0,2) 3C:(2,2,2)
1A:(0,0,0) 2L:(2,2,1) 4L:(0,1,0) 5D:(0,2,0) 6H:(2,1,1) 7E:(0,1,2) 3C:(2,2,2)
1A:(0,0,0) 2L:(2,2,1) 5G:(1,2,0) 4B:(2,1,1) 6A:(1,0,1) 7F:(1,0,2) 3D:(0,2,2)
1A:(0,0,0) 2L:(2,2,1) 7A:(0,1,0) 4F:(0,0,1) 5A:(1,1,1) 6B:(2,0,1) 3G:(0,0,2)
1A:(0,0,0) 2L:(2,2,1) 5F:(2,0,1) 7A:(0,1,0) 4F:(0,0,1) 6I:(1,2,1) 3G:(0,0,2)
1A:(0,0,0) 2L:(2,2,1) 4F:(2,0,1) 7A:(0,1,0) 6B:(1,1,1) 5A:(0,0,1) 3G:(0,0,2)
1A:(0,0,0) 2L:(2,2,1) 4F:(2,0,1) 7A:(0,1,0) 6F:(0,0,1) 3G:(0,0,2) 5K:(1,2,1)
1A:(0,0,0) 2L:(2,2,1) 7A:(0,1,0) 5A:(1,1,1) 6B:(2,0,1) 4E:(0,0,1) 3H:(0,0,2)
1A:(0,0,0) 2L:(2,2,1) 5F:(2,0,1) 7A:(0,1,0) 4E:(0,0,1) 6I:(1,2,1) 3H:(0,0,2)
1A:(0,0,0) 2L:(2,2,1) 6F:(0,1,0) 4B:(2,0,1) 5I:(0,0,1) 7E:(0,1,2) 3H:(2,0,2)
1A:(0,0,0) 2L:(2,2,1) 7A:(0,1,0) 6B:(1,1,1) 5A:(0,0,1) 4G:(2,0,1) 3H:(2,0,2)
1A:(0,0,0) 2L:(2,2,1) 7A:(0,1,0) 6F:(0,0,1) 4G:(2,0,1) 5K:(1,2,1) 3H:(2,0,2)
1A:(0,0,0) 7A:(0,1,0) 5F:(1,0,1) 6B:(2,1,0) 3D:(0,2,2) 4J:(2,0,0) 2M:(0,0,1)
1A:(0,0,0) 5C:(2,1,0) 6F:(0,1,0) 7B:(1,1,1) 2M:(0,0,1) 4L:(2,2,0) 3D:(0,2,2)
1A:(0,0,0) 5C:(2,1,0) 7A:(0,1,0) 2M:(0,0,1) 4L:(2,2,0) 6H:(1,2,1) 3D:(0,2,2)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 4B:(2,0,1) 5K:(1,2,1) 6L:(2,2,1) 2M:(0,0,1)
1A:(0,0,0) 3F:(2,0,0) 6F:(0,1,0) 7H:(1,2,2) 4B:(2,0,1) 5L:(0,2,1) 2M:(0,0,1)
1A:(0,0,0) 5C:(2,1,0) 6F:(0,1,0) 7B:(1,1,1) 2M:(0,0,1) 3L:(2,2,0) 4B:(2,1,2)
1A:(0,0,0) 5C:(2,1,0) 7A:(0,1,0) 2M:(0,0,1) 3L:(2,2,0) 6H:(1,2,1) 4B:(2,1,2)
1A:(0,0,0) 5C:(2,1,0) 6F:(0,1,0) 2M:(0,0,1) 3L:(2,2,0) 4E:(0,1,1) 7E:(0,1,2)
1A:(0,0,0) 5C:(2,1,0) 6F:(0,1,0) 7A:(0,0,1) 3B:(2,0,2) 4L:(2,2,0) 2M:(0,2,1)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 6I:(0,1,0) 7F:(1,0,2) 2M:(0,2,1) 5J:(2,0,1)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 7E:(0,0,1) 2M:(0,2,1) 5J:(2,0,1) 6K:(1,0,1)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 6I:(0,1,0) 7F:(1,0,2) 2M:(0,2,1) 5J:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 7E:(0,0,1) 2M:(0,2,1) 5J:(2,0,1) 6K:(1,0,1)
1A:(0,0,0) 3F:(2,0,0) 4H:(0,2,0) 6K:(1,0,1) 7E:(1,1,1) 2M:(0,2,1) 5J:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 6F:(0,1,0) 4D:(1,0,1) 5K:(2,2,1) 7G:(2,1,2) 2N:(0,0,1)
1A:(0,0,0) 4K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5A:(0,1,0) 6A:(0,1,1) 2N:(0,0,1)
1A:(0,0,0) 4K:(2,0,0) 6D:(0,2,0) 7D:(1,2,0) 3H:(2,0,2) 5D:(0,2,1) 2N:(0,0,1)
1A:(0,0,0) 3K:(2,0,0) 6D:(0,2,0) 7D:(1,2,0) 4E:(0,2,1) 5K:(2,1,1) 2N:(0,0,1)
1A:(0,0,0) 6B:(2,0,0) 7A:(0,1,0) 4K:(2,2,0) 5H:(0,1,1) 2N:(2,0,1) 3A:(0,0,2)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 6I:(0,1,0) 7E:(0,1,2) 2N:(2,0,1) 5I:(0,0,1)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 5L:(0,1,0) 6L:(1,1,1) 7E:(0,1,2) 2N:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 6I:(0,1,0) 7E:(0,1,2) 2N:(2,0,1) 5I:(0,0,1)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 5L:(0,1,0) 6L:(1,1,1) 7E:(0,1,2) 2N:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 4F:(0,0,1) 5C:(1,1,1) 6C:(2,2,1) 2N:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 4G:(2,2,1) 5I:(1,1,1) 6G:(1,0,1) 2O:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 4A:(0,0,1) 5J:(2,0,1) 6K:(1,0,1) 2O:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 6F:(0,1,0) 4D:(1,0,1) 5J:(2,0,1) 7F:(1,0,2) 2O:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 4H:(0,2,0) 6K:(1,0,1) 7H:(0,2,1) 2O:(2,2,1) 5J:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 5E:(0,0,1) 6F:(0,1,0) 7G:(2,1,2) 4H:(0,2,1) 2O:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 6F:(0,1,0) 7C:(1,1,1) 4H:(0,2,1) 5J:(2,0,1) 2O:(2,2,1)
1A:(0,0,0) 3K:(2,0,0) 6E:(1,2,0) 5A:(0,1,0) 7A:(0,0,1) 2O:(2,2,1) 4C:(0,0,2)
1A:(0,0,0) 3K:(2,0,0) 6E:(1,2,0) 5A:(0,1,0) 2O:(2,2,1) 4E:(0,1,1) 7F:(1,0,2)
1A:(0,0,0) 3E:(0,2,0) 4F:(2,0,0) 5L:(0,1,0) 6J:(1,1,1) 7G:(2,1,2) 2P:(0,2,1)
1A:(0,0,0) 3F:(2,0,0) 4E:(0,2,0) 5L:(0,1,0) 6J:(1,1,1) 7G:(2,1,2) 2P:(0,2,1)
1A:(0,0,0) 4H:(0,2,0) 7D:(1,2,0) 2P:(0,2,1) 3J:(2,0,0) 5A:(1,1,1) 6J:(1,0,1)
1A:(0,0,0) 3K:(2,0,0) 4H:(0,2,0) 5F:(2,1,0) 6B:(2,1,1) 7E:(1,0,2) 2P:(0,2,1)
1A:(0,0,0) 3K:(2,0,0) 4H:(0,2,0) 5F:(2,1,0) 6C:(2,1,1) 7H:(1,2,2) 2P:(0,2,1)
1A:(0,0,0) 3E:(0,2,0) 4L:(0,1,0) 6B:(2,0,0) 7E:(0,1,2) 5B:(2,0,1) 2P:(2,2,1)
1A:(0,0,0) 3E:(0,2,0) 4L:(0,1,0) 5C:(2,1,0) 6C:(2,1,1) 7E:(0,1,2) 2P:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 6F:(0,1,0) 4B:(2,0,1) 5I:(0,0,1) 7E:(0,1,2) 2P:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 6B:(1,1,1) 5A:(0,0,1) 4G:(2,0,1) 2P:(2,2,1)
1A:(0,0,0) 3F:(2,0,0) 7A:(0,1,0) 6F:(0,0,1) 4G:(2,0,1) 5K:(1,2,1) 2P:(2,2,1)
1A:(0,0,0) 2Q:(0,2,0) 4J:(0,1,0) 5C:(2,1,0) 6L:(2,2,0) 7F:(1,0,2) 3C:(2,2,2)
1A:(0,0,0) 2Q:(0,2,0) 3F:(2,0,0) 4J:(0,1,0) 5H:(1,1,1) 6L:(2,2,1) 7F:(1,0,2)
1A:(0,0,0) 2Q:(0,2,0) 3K:(2,0,0) 4J:(0,1,0) 5C:(2,2,0) 6L:(2,2,1) 7F:(1,0,2)
1A:(0,0,0) 2Q:(0,2,0) 4J:(0,1,0) 5C:(2,1,0) 7F:(1,0,2) 3L:(2,2,0) 6I:(1,1,1)
1A:(0,0,0) 2Q:(1,2,0) 4H:(0,2,0) 5C:(2,1,0) 6L:(2,1,1) 7D:(0,2,1) 3A:(0,0,2)
1A:(0,0,0) 2Q:(1,2,0) 4I:(0,2,0) 5C:(2,1,0) 6L:(2,1,1) 7E:(0,0,1) 3A:(0,0,2)
1A:(0,0,0) 2Q:(1,2,0) 4I:(0,2,0) 5L:(0,1,0) 6B:(2,0,0) 7G:(2,1,2) 3A:(0,0,2)
1A:(0,0,0) 2Q:(1,2,0) 3I:(0,2,0) 5C:(2,1,0) 6L:(2,1,1) 7E:(0,0,1) 4A:(0,0,2)
1A:(0,0,0) 2Q:(1,2,0) 3I:(0,2,0) 5L:(0,1,0) 6B:(2,0,0) 7G:(2,1,2) 4A:(0,0,2)
1A:(0,0,0) 2Q:(1,2,0) 3I:(0,2,0) 4L:(0,1,0) 5C:(2,1,0) 6L:(2,1,1) 7G:(1,2,2)
1A:(0,0,0) 2R:(0,1,0) 6G:(1,0,1) 7D:(1,2,0) 4J:(2,0,0) 5A:(1,1,1) 3B:(2,0,2)
1A:(0,0,0) 2R:(0,1,0) 3F:(2,0,0) 4I:(1,2,0) 6A:(0,1,1) 5B:(1,0,1) 7G:(2,1,2)
1A:(0,0,0) 2R:(0,1,0) 3F:(2,0,0) 4I:(1,2,0) 6H:(1,1,1) 7G:(2,1,2) 5I:(0,1,1)
1A:(0,0,0) 2R:(0,1,0) 4K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5E:(0,1,1) 6J:(0,0,1)
1A:(0,0,0) 2R:(0,1,0) 4K:(2,0,0) 5G:(1,1,1) 7D:(1,2,0) 3H:(2,0,2) 6L:(1,2,1)
1A:(0,0,0) 2R:(0,1,0) 6G:(1,0,1) 7D:(1,2,0) 3J:(2,0,0) 5A:(1,1,1) 4C:(0,0,2)
1A:(0,0,0) 2R:(0,1,0) 3K:(2,0,0) 5F:(2,1,0) 6B:(2,1,1) 7A:(0,0,1) 4C:(0,0,2)
1A:(0,0,0) 2R:(0,1,0) 3K:(2,0,0) 5F:(2,1,0) 6D:(0,1,1) 7C:(2,2,1) 4C:(0,1,2)
1A:(0,0,0) 2R:(0,1,0) 3K:(2,0,0) 6D:(0,1,1) 7D:(1,2,0) 5H:(1,2,1) 4C:(0,1,2)
1A:(0,0,0) 2R:(0,1,0) 3K:(2,0,0) 5F:(2,1,0) 6B:(2,1,1) 4E:(0,1,1) 7F:(1,0,2)
1A:(0,0,0) 2R:(0,1,0) 3K:(2,0,0) 5F:(2,1,0) 6D:(0,1,1) 4G:(2,1,1) 7H:(1,2,2)
1A:(0,0,0) 2R:(0,1,0) 5C:(2,1,0) 6L:(1,2,0) 7F:(1,0,2) 3L:(2,2,0) 4D:(2,0,2)
1A:(0,0,0) 2R:(2,1,0) 4J:(2,0,0) 7A:(0,1,0) 6B:(1,1,1) 5A:(0,0,1) 3G:(0,0,2)
1A:(0,0,0) 2R:(2,1,0) 4J:(2,0,0) 7A:(0,1,0) 6F:(0,0,1) 3G:(0,0,2) 5K:(1,2,1)
1A:(0,0,0) 2R:(2,1,0) 3J:(2,0,0) 4L:(0,1,0) 5D:(0,2,0) 6J:(1,0,1) 7E:(0,1,2)
1A:(0,0,0) 2R:(2,1,0) 3K:(2,0,0) 5D:(0,2,0) 6K:(2,1,1) 4J:(0,1,0) 7F:(1,0,2)
1A:(0,0,0) 2S:(1,2,0) 3F:(2,0,0) 5L:(0,1,0) 6F:(1,1,1) 7G:(2,1,2) 4A:(0,0,2)
1A:(0,0,0) 2S:(1,2,0) 3K:(2,0,0) 4I:(0,1,0) 6B:(2,1,0) 7F:(1,0,2) 5J:(2,1,1)
1A:(0,0,0) 2S:(1,2,0) 3K:(2,0,0) 4L:(0,1,0) 6B:(2,1,0) 7H:(0,1,2) 5J:(2,1,1)
1A:(0,0,0) 2S:(1,2,0) 3K:(2,2,0) 5C:(2,1,0) 6L:(2,1,1) 7E:(0,0,1) 4A:(0,0,2)
1A:(0,0,0) 2S:(1,2,0) 3K:(2,2,0) 5L:(0,1,0) 6B:(2,0,0) 7G:(2,1,2) 4A:(0,0,2)
1A:(0,0,0) 2S:(1,2,0) 3K:(2,2,0) 4L:(0,1,0) 5C:(2,1,0) 6L:(2,1,1) 7G:(1,2,2)
1A:(0,0,0) 2T:(0,2,0) 3F:(2,0,0) 4K:(1,2,0) 6H:(1,1,1) 7G:(2,1,2) 5K:(2,2,1)
1A:(0,0,0) 2T:(2,1,0) 7A:(0,1,0) 4K:(2,2,0) 5H:(0,1,1) 6A:(1,1,1) 3A:(0,0,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4J:(0,1,0) 6B:(2,1,1) 5A:(1,0,1) 7F:(1,0,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4J:(0,1,0) 5B:(1,0,1) 6B:(2,1,1) 7E:(1,0,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4J:(0,1,0) 5B:(1,0,1) 6C:(2,1,1) 7H:(1,2,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4J:(0,1,0) 5G:(2,1,1) 6J:(0,0,1) 7H:(1,2,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4J:(0,1,0) 6F:(1,0,1) 7F:(1,0,2) 5K:(2,2,1)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4L:(0,1,0) 5E:(1,1,1) 6J:(1,0,1) 7E:(0,1,2)
1A:(0,0,0) 2T:(2,1,0) 3E:(0,2,0) 4L:(0,1,0) 5G:(2,1,1) 6L:(2,2,1) 7E:(0,1,2)
1A:(0,0,0) 2T:(2,1,0) 4L:(2,2,0) 7A:(0,1,0) 5A:(1,1,1) 6A:(0,0,1) 3H:(0,0,2)
1A:(0,0,0) 2T:(2,1,0) 7A:(0,1,0) 3K:(2,2,0) 4F:(0,0,1) 5C:(1,1,1) 6K:(2,1,1)
1A:(0,0,0) 2T:(2,1,0) 3L:(2,2,0) 4L:(0,1,0) 5D:(0,2,0) 6J:(1,0,1) 7E:(0,1,2)
1A:(0,0,0) 2T:(2,2,0) 3K:(2,0,0) 4I:(1,2,0) 6D:(0,2,0) 7E:(0,1,2) 5I:(0,0,1)
1A:(0,0,0) 2T:(2,2,0) 3K:(2,0,0) 6D:(0,2,0) 7F:(1,0,2) 4K:(1,2,0) 5K:(2,2,1)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 2U:(1,0,2) 4I:(0,2,0) 6A:(1,1,1) 3A:(0,0,2)
1A:(0,0,0) 3E:(0,2,0) 4J:(0,1,0) 5K:(2,1,0) 6J:(0,0,1) 7H:(1,2,2) 2U:(1,0,2)
1A:(0,0,0) 3E:(0,2,0) 4L:(0,1,0) 5K:(2,1,0) 6L:(2,2,1) 7E:(0,1,2) 2U:(1,0,2)
1A:(0,0,0) 5L:(0,1,0) 7D:(1,2,0) 2U:(1,0,2) 3I:(0,2,0) 6A:(1,1,1) 4A:(0,0,2)
1A:(0,0,0) 4I:(0,1,0) 5B:(1,0,1) 6E:(1,2,0) 2U:(1,0,2) 3I:(0,2,0) 7H:(1,2,2)
1A:(0,0,0) 4L:(0,1,0) 6B:(1,0,1) 7D:(1,2,0) 2U:(1,0,2) 3I:(0,2,0) 5J:(2,1,1)
1A:(0,0,0) 5C:(2,1,0) 6L:(2,1,1) 7A:(0,1,0) 4A:(0,0,1) 2U:(1,2,2) 3A:(0,0,2)
1A:(0,0,0) 4H:(0,2,0) 5C:(2,1,0) 6L:(2,1,1) 7H:(0,2,1) 2U:(1,2,2) 3A:(0,0,2)
1A:(0,0,0) 4L:(0,1,0) 7D:(1,2,0) 2V:(0,1,2) 3J:(2,0,0) 5A:(1,1,1) 6J:(1,0,1)
1A:(0,0,0) 3K:(2,0,0) 5F:(2,1,0) 6B:(2,1,1) 7E:(0,0,1) 2V:(0,1,2) 4C:(0,0,2)
1A:(0,0,0) 3K:(2,0,0) 4L:(0,1,0) 5F:(2,1,0) 6B:(2,1,1) 7E:(1,0,2) 2V:(0,1,2)
1A:(0,0,0) 3K:(2,0,0) 4L:(0,1,0) 5F:(2,1,0) 6C:(2,1,1) 7H:(1,2,2) 2V:(0,1,2)
1A:(0,0,0) 3E:(0,2,0) 4J:(0,1,0) 6K:(2,0,0) 7F:(1,0,2) 2V:(2,0,2) 5K:(2,2,1)
1A:(0,0,0) 5C:(2,1,0) 7A:(0,1,0) 4F:(0,0,1) 6G:(2,1,1) 2V:(2,1,2) 3B:(2,0,2)
1A:(0,0,0) 3K:(2,0,0) 4K:(2,1,0) 6F:(0,1,0) 2V:(2,1,2) 5A:(0,1,1) 7F:(1,0,2)
1A:(0,0,0) 3K:(2,0,0) 4K:(2,1,0) 7A:(0,1,0) 2V:(2,1,2) 6D:(0,1,1) 5K:(1,2,1)
1A:(0,0,0) 3F:(2,0,0) 4I:(1,2,0) 6I:(0,1,0) 7F:(1,0,2) 2W:(1,2,2) 5J:(2,0,1)
1A:(0,0,0) 3F:(2,0,0) 4I:(1,2,0) 7E:(0,0,1) 2W:(1,2,2) 5J:(2,0,1) 6K:(1,0,1)
1A:(0,0,0) 4K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 5I:(0,1,0) 6J:(0,0,1) 2W:(1,2,2)
1A:(0,0,0) 3K:(2,0,0) 4I:(0,1,0) 6E:(1,2,0) 7F:(1,0,2) 5D:(1,2,1) 2W:(1,2,2)
1A:(0,0,0) 3K:(2,0,0) 4L:(0,1,0) 6E:(1,2,0) 7H:(0,1,2) 5D:(1,2,1) 2W:(1,2,2)
1A:(0,0,0) 6K:(2,0,0) 7D:(1,2,0) 3H:(2,0,2) 4I:(0,2,0) 5I:(0,0,1) 2X:(0,2,2)
1A:(0,0,0) 3K:(2,0,0) 7D:(1,2,0) 4I:(0,2,0) 6A:(1,1,1) 2X:(0,2,2) 5I:(0,0,1)
1A:(0,0,0) 7A:(0,1,0) 6B:(2,1,0) 4C:(0,0,1) 5L:(0,1,1) 2X:(2,1,2) 3D:(0,2,2)
1A:(0,0,0) 3E:(0,2,0) 4J:(2,1,0) 6I:(0,1,0) 7E:(0,1,2) 2X:(2,1,2) 5I:(0,0,1)
1A:(0,0,0) 3E:(0,2,0) 4J:(2,1,0) 5L:(0,1,0) 6L:(1,1,1) 7E:(0,1,2) 2X:(2,1,2)
2B:(2,1,0) 4B:(2,0,0) 1A:(0,1,1) 3I:(0,0,0) 5C:(2,1,1) 6L:(2,2,1) 7E:(0,1,2)
2B:(2,1,0) 4B:(2,0,0) 1A:(0,1,1) 3I:(0,0,0) 5L:(0,2,1) 6B:(2,1,1) 7G:(2,1,2)
2C:(1,2,0) 3C:(2,2,0) 4K:(1,0,0) 5C:(2,1,1) 1A:(0,1,1) 6L:(2,2,1) 7E:(0,1,2)
2C:(1,2,0) 3C:(2,2,0) 4K:(1,0,0) 1A:(0,1,1) 5L:(0,2,1) 6B:(2,1,1) 7G:(2,1,2)
2D:(0,1,0) 3D:(0,2,0) 4J:(2,1,0) 1A:(0,1,1) 5B:(1,0,1) 6I:(0,2,1) 7G:(2,1,2)
2D:(0,1,0) 3D:(0,2,0) 4J:(2,1,0) 6A:(1,0,1) 1A:(0,1,1) 5I:(0,0,1) 7E:(0,1,2)
2D:(0,1,0) 4B:(2,1,0) 1A:(0,1,1) 3L:(2,2,0) 5B:(1,0,1) 6I:(0,2,1) 7G:(2,1,2)
2D:(0,1,0) 4B:(2,1,0) 1A:(0,1,1) 3L:(2,2,0) 6A:(1,0,1) 7E:(0,1,2) 5I:(0,0,1)
2I:(0,2,1) 5G:(1,1,0) 7C:(2,1,0) 1A:(0,1,1) 4H:(2,2,1) 6K:(1,0,1) 3D:(0,2,2)
2I:(0,2,1) 5H:(0,1,0) 6E:(1,1,0) 1A:(0,1,1) 4H:(2,2,1) 7F:(1,0,2) 3D:(0,2,2)
2J:(0,0,1) 5E:(1,0,0) 6F:(1,1,0) 1A:(0,1,1) 4G:(2,0,1) 7E:(0,1,2) 3C:(2,2,2)
2J:(2,0,1) 4H:(2,2,1) 5F:(1,1,0) 7B:(1,0,0) 1A:(0,1,1) 3D:(0,2,2) 6K:(1,0,1)
2Q:(1,0,0) 4I:(0,0,0) 6G:(1,1,0) 7D:(1,2,0) 1A:(0,1,1) 3A:(0,0,2) 5J:(2,1,1)
2Q:(1,0,0) 3I:(0,0,0) 6G:(1,1,0) 7D:(1,2,0) 1A:(0,1,1) 4D:(1,0,2) 5J:(2,1,1)
2R:(0,1,0) 5H:(1,1,0) 6E:(1,2,0) 1A:(0,1,1) 3I:(0,0,0) 4B:(2,0,2) 7H:(1,2,2)
2R:(0,1,0) 6F:(1,1,0) 7C:(2,1,0) 1A:(0,1,1) 3I:(0,0,0) 4B:(2,0,2) 5J:(2,1,1)
2R:(0,1,0) 5E:(1,0,0) 6F:(1,1,0) 1A:(0,1,1) 3I:(0,0,0) 4C:(0,1,2) 7G:(2,1,2)
2R:(0,1,0) 5H:(1,1,0) 7D:(1,2,0) 1A:(0,1,1) 3I:(0,0,0) 4C:(0,1,2) 6L:(2,1,1)
2R:(2,1,0) 3J:(2,0,0) 5F:(1,1,0) 7B:(1,0,0) 1A:(0,1,1) 4B:(2,1,2) 6K:(1,0,1)
2A:(1,0,0) 3A:(0,0,0) 4I:(1,2,0) 5A:(0,1,1) 1A:(1,0,1) 6I:(1,1,1) 7F:(1,0,2)
2A:(1,0,0) 4E:(0,2,0) 6F:(0,0,0) 1A:(1,0,1) 3C:(2,2,2) 5A:(0,1,1) 7F:(1,0,2)
2B:(2,1,0) 3B:(2,0,0) 4L:(0,1,0) 6C:(1,2,1) 1A:(1,0,1) 5L:(1,1,1) 7H:(1,2,2)
2B:(2,1,0) 4B:(2,0,0) 6J:(0,0,0) 1A:(1,0,1) 3B:(2,0,2) 5D:(1,2,1) 7E:(0,1,2)
2B:(2,1,0) 4B:(2,0,0) 1A:(1,0,1) 3J:(0,0,0) 5L:(1,1,1) 6C:(1,2,1) 7H:(1,2,2)
2D:(0,1,0) 4B:(2,1,0) 5K:(2,2,0) 1A:(1,0,1) 3C:(2,2,2) 6D:(0,1,1) 7E:(0,1,2)
2D:(0,1,0) 6H:(2,2,0) 1A:(1,0,1) 4E:(0,2,0) 5A:(0,1,1) 7F:(1,0,2) 3C:(2,2,2)
2D:(0,1,0) 4B:(2,1,0) 1A:(1,0,1) 3K:(2,2,0) 5A:(0,1,1) 6I:(1,1,1) 7F:(1,0,2)
2I:(0,0,1) 6H:(2,2,0) 7A:(0,1,0) 1A:(1,0,1) 4G:(2,2,1) 5L:(0,1,1) 3C:(2,2,2)
2I:(0,2,1) 4G:(2,2,1) 5F:(2,0,0) 6G:(1,0,0) 1A:(1,0,1) 3C:(2,2,2) 7F:(1,0,2)
2Q:(1,2,0) 3I:(0,2,0) 5F:(2,0,0) 6G:(1,0,0) 1A:(1,0,1) 4D:(2,0,2) 7F:(1,0,2)
2R:(0,1,0) 3B:(2,0,0) 5G:(1,1,1) 7D:(1,2,0) 1A:(1,0,1) 4B:(2,0,2) 6I:(1,2,1)
2R:(0,1,0) 4J:(0,0,0) 5F:(2,1,0) 6G:(2,0,0) 1A:(1,0,1) 3B:(2,0,2) 7H:(1,2,2)
2R:(0,1,0) 3J:(0,0,0) 5F:(2,1,0) 6G:(2,0,0) 1A:(1,0,1) 4B:(2,0,2) 7H:(1,2,2)
Many thanks to my colleagues Mouna and Mariem for their precious help in this project.